ECUACIONES Y DESIGUALDADES

                 Graficando Desigualdades Lineales

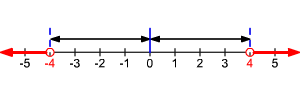
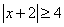
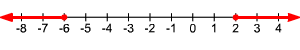  Las desigualdades lineales pueden graficarse en un plano de coordenadas. Las soluciones de una desigualdad lineal son una región del plano coordenado. Una recta límite, que es la ecuación lineal relacionada, sirve como frontera para la región. Puedes usar una representación visual para encontrar los valores que hacen válida a la desigualdad — y también los que la hacen inválida. Veamos las desigualdades volviendo al plano de coordenadas.




        Desigualdades Lineales como Regiones

   Las desigualdades lineales son diferentes a las ecuaciones lineales, si bien puedes aplicar lo que sabes sobre ecuaciones para ayudarte a entender las desigualdades. Las desigualdades y las ecuaciones son enunciados matemáticos que comparan dos valores. Las ecuaciones usan el símbolo =; las desigualdades se representan con los símbolos <, ≤, >, y ≥.

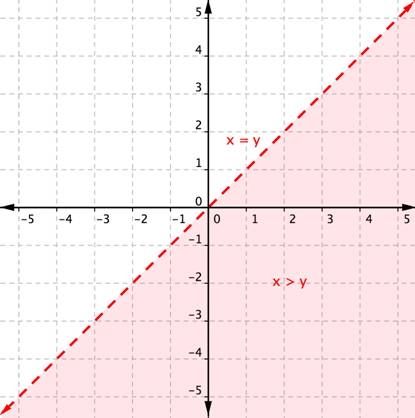
   Una manera de visualizar desigualdades de dos variables es graficarlas en el plano de coordenadas. Así es como se ve la desigualdad x > y. La solución es la región sombreada.

  Hay algunas cosas que debemos notar. Primero, observa la recta límite roja y punteada: esta es la gráfica de la ecuación lineal relacionada x = y. Segundo, observa la región roja a la derecha de la recta. Esta región (excluyendo la recta x = y) representa el conjunto de soluciones de la desigualdad x > y. ¿Recuerdas que todos los puntos en la recta son soluciones de la ecuación lineal de una recta? Bueno, todos los puntos en una región son soluciones de la desigualdad lineal que representa esa región.

Pensemos en esto un momento — si x > y, entonces una gráfica de x > y mostrará todos los pares ordenados (x, y) donde la coordenada-x es mayor que la coordenada-y.

La gráfica de abajo muestra la región x > y así como algunos pares ordenados en el plano de coordenadas. Observa cada par ordenado. ¿Es la coordenada-x mayor que la coordenada-y? ¿Está el par ordenado dentro o fuera de la región sombreada?

                                               

  Los pares ordenados (4, 0) y (0, −3) están dentro de la región sombreada. En estos pares ordenados, la coordenada-x es más grande que la coordenada-y. Estos pares ordenados están en el conjunto solución de la ecuación x > y.

  Los pares ordenados (−3, 3) y (2, 3) están fuera de la región sombreada. En estos pares ordenados, la coordenada-x es más pequeña que la coordenada-y, por lo que no están incluidos en el conjunto solución de la desigualdad.

  El par ordenado (−2, −2) está en la recta límite. No es una solución porque −2 no es mayor que −2. Sin embargo, si la desigualdad hubiera sido x ≥ y (se lee como “x es mayor o igual que y"), entonces (−2, −2) habría sido incluido (y la recta habría sido representada por una línea sólida, no una línea punteada).

  Veamos otro ejemplo: la desigualdad 3x + 2y ≤ 6. LA gráfica siguiente muestra la región de valores que vuelve la desigualdad válida (rojo sombreado), la recta límite 3x + 2y = 6, así como un grupo de pares ordenados. Esta vez, a recta límite es sólida, porque puntos en la recta límite 3x + 2y = 6 también son válidos en la ecuación 3x + 2y ≤ 6.

                                                    

   Como hiciste en el ejemplo anterior, puedes sustituir los valores de x y, y en cada uno de los pares ordenados (x, y), en la desigualdad para encontrar soluciones. Si bien pudiste hacerlo en la mente para la desigualdad x > y, a veces construir una tabla de valores tiene sentido para desigualdades más complicadas.

Par Ordenado	Hace a la desigualdad 3 x + 2y ≤ 6 un enunciado válido	Hace la desigualdad 3 x + 2y ≤ 6 un enunciado inválido
(−5, 5)	3(−5) + 2(5) ≤ 6 −15 +10 ≤ 6 −5 ≤ 6
(−2, −2)	3(−2) + 2(–2) ≤ 6 −6 + (−4) ≤ 6 –10 ≤ 6
(2, 3)		3(2) + 2(3) ≤ 6 6 + 6 ≤ 6 12 ≤ 6
(2, 0)	3(2) + 2(0) ≤ 6 6 + 0 ≤ 6 6 ≤ 6
(4, −1)		3(4) + 2(−1) ≤ 6 12 + (−2) ≤ 6 10 ≤ 6

  

   Si sustituimos (x, y) en la desigualdad y obtenemos un enunciado válido, entonces el par ordenado es una solución de la desigualdad, y el punto estará graficado dentro de la región sombreada o será parte de la recta límite sólida. Un enunciado falso significa que el par ordenado no es una solución, y el punto estará fuera de la región sombreada, o será parte de una recta límite punteada.

Ejemplo
Problema	Usa la gráfica para determinar qué pares ordenados son soluciones de la desigualdad x – y < 3.
		Las soluciones estarán localizadas en la región sombreada. Como este es un problema de “menor que”, los pares ordenados en la recta límite no están incluidos en el conjunto solución.
	(−1, 1) (−2, −2)	Estos valores están localizados en la región sombreada, por lo que son soluciones (Cuando se sustituyen en la desigualdad x – y < 3, producen enunciados válidos.)
	(1, −2) (3, −2) (4, 0)	Estos valores no están localizados en la región sombreada, por lo que no son soluciones (Cuando se sustituyen en la desigualdad x – y < 3, producen enunciados inválidos.)
Respuesta	(−1, 1), (−2, −2)

Ejemplo
Problema	¿Es (2, −3) una solución de la desigualdad y < −3x + 1?
	y < −3x + 1	Si (2, −3) es una solución, entonces dará un enunciado válido cuando se sustituye en la desigualdad y < −3x + 1.
	−3 < −3(2) + 1	Sustituye x = 2 y y = −3 en la desigualdad.
	−3 < −6 + 1	Evalúa.
	−3 < −5	Este enunciado no es válido, por lo que el par ordenado (2, −3) no es una solución.
Respuesta	(2, −3) no es una solución.

                                   

¿Qué par ordenado es una solución de la desigualdad 2y - 5x < 2? A) (−5, 1) B) (−3, 3) C) (1, 5) D) (3, 3) Mostrar/Ocultar Respuesta

                
                     Graficando Desigualdades

   Entonces ¿cómo pasas de la forma algebraica de una desigualdad, como y > 3x + 1, a la gráfica de esa desigualdad? Graficar desigualdades es fácil si sigues un par de pasos.

Graficando Desigualdades Para graficar una desigualdad: o        Gráfica la recta límite relacionada. Reemplaza el signo <, >, ≤ o ≥ en la desigualdad por el signo = para obtener la ecuación de la recta límite. o        Identifica por lo menos un par ordenado en cada lado de la recta límite y sustituye esos valores (x, y) en la desigualdad. Sombrea la región que contiene los pares ordenados que hacen válida la desigualdad. o        Si hay puntos en la recta límite que son soluciones, entonces usa una línea sólida para representar la recta límite. Esto pasará con las desigualdades ≤ o ≥. o        Si hay puntos en la recta límite que no son soluciones, entonces usa una línea punteada para representar la recta límite. Esto pasará con las desigualdades < o >.

Grafiquemos la desigualdad x + 4y ≤ 4.

Para graficar la recta límite, encuentra por lo menos dos valores que estén en la recta x + 4y = 4. Puedes usar las intersecciones en xy, después para esta ecuación primero sustituye 0 por x, cuando encuentres el valor de y; sustituye 0 por el valor de y, entonces encuentra x.

x	y
0	1
4	0

Grafica los puntos (0, 1) y (4, 0), y dibuja una recta que pase por esos dos puntos para la recta límite. La línea es sólida porque ≤ significa “menor o igual que,” por lo que todos los pares ordenados sobre la recta están incluidos en el conjunto solución.

 

    El siguiente paso es encontrar la región que contiene las soluciones. ¿Está arriba o abajo de la recta límite? Para identificar la región donde la desigualdad es válida, puedes probar con un par de pares ordenados, uno en cada lado de la recta límite.

Si sustituyes (−1, 3) en x + 4y ≤ 4:

−1 + 4(3) ≤ 4

−1 + 12 ≤ 4

11 ≤ 4

Este es un enunciado falso, porque 11 no es menor o igual que 4.

Por otro lado, si sustituyes (2, 0) en x + 4y ≤ 4:

2 + 4(0) ≤ 4

2 + 0 ≤ 4

2 ≤ 4

¡Esto es válido! La región que incluye (2, 0) debe ser sombreada, porque es la región de soluciones.

 

Y ya lo tienes — la gráfica del conjunto de soluciones de x + 4y ≤ 4.

Ejemplo
Problema	Gráfica la desigualdad 2y > 4x – 6.
		Despeja y.
	x y 0 −3 2 1	Crea una tabla de valores para encontrar dos puntos en la recta , o grafica basado en el método pendiente-intersección, el valor de b de la intersección en y es -3 y la pendiente es 2. Grafica los puntos, y grafica la recta. La recta es punteada porque el signo de la desigualdad es >, y no ≥ por lo tanto los puntos en la recta no son soluciones de la desigualdad.
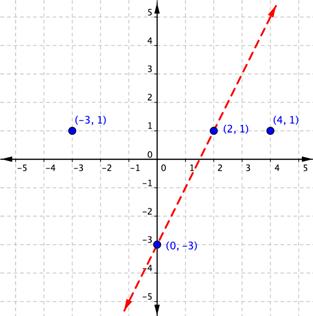	2y > 4x – 6 Prueba 1: (−3, 1) 2(1) > 4(−3) – 6 2 > –12 – 6 2 > −18 ¡Válido! Prueba 2: (4, 1) 2(1) > 4(4) – 6 2 > 16 – 6 2 > 10 ¡Inválido!	Encuentra un par ordenado en cada lado de la recta límite, Inserta los valores de x y y en la desigualdad 2y > 4x – 6 y ve qué par ordenado resulta en un enunciado válido. Como (−3, 1) resulta en un enunciado válido, la región que incluye (−3, 1) debe ser sombreada.
Respuesta	La gráfica de la desigualdad 2y > 4x – 6 es:

            

          Desigualdades de valor absoluto (<)

      La desigualdad | x | < 4 significa que la distancia entre x y 0 es menor que 4.

                    

    Así, x > -4 Y x < 4. El conjunto solución es  .

Cuando se resuelven desigualdades de valor absoluto, hay dos casos a considerar.

Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.

Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.

La solución es la intersección de las soluciones de estos dos casos.

En otras palabras, para cualesquiera números reales a y b , si | a | < b , entonces a < b Y a > - b 

Ejemplo 1 :

Resuelva y grafique.

| x – 7| < 3

  Para resolver este tipo de desigualdad, necesitamos descomponerla en una desigualdad compuesta .

x – 7 < 3 Y x – 7 > –3

–3 < x – 7 < 3

Sume 7 en cada expresión.

-3 + 7 < x - 7 + 7 < 3 + 7

4 < x <10

La gráfica se vería así:

                                 

              Desigualdades de valor absoluto (>)

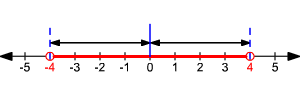
    La desigualdad | x | > 4 significa que la distancia entre x y 0 es mayor que 4.

                                      

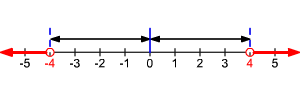
     Así, x < -4 O x > 4. El conjunto solución es  .

Cuando se resuelven desigualdades de valor absoluto, hay dos casos a considerar.

Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.

Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.

   En otras palabras, para cualesquiera números reales a y b , si | a | > b , entonces a > b O a < - b .

Ejemplo 2 :

Resuelva y grafique.

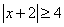
  Separe en dos desigualdades.

  Reste 2 de cada lado en cada desigualdad.

La gráfica se vería así:

.

        

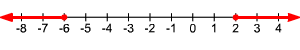                                         Desigualdades cuadráticas

   Una inecuación cuadrática es una ecuación de la forma ax² + bx + c > 0, o ax² + bx + c < 0, o también si se manejan las desigualdades mayor igual o menor igual, donde a, b, y , c son números reales y a es un número diferente de cero

                      

                                                    Aplicación en la vida                        

  Hay muchos casos de aplicación de desigualdades en la vida, eso incluye áreas de la tecnología, la medicina, la economía y otras.

Por ejemplo, en la economía las desigualdades aparecen en el análisis de proyectos para ver que propuesta es más viable para realizar inversiones. Esto se hace resolviendo una desigualdad con valores llamados TIR y TIO (tasa interna de retorno y tasa interna de oportunidad).
En la medicina, toda la parte de dosimetría y radiometría se basa en desigualdades (menos que esto, mas que esto, y sino los pacientes podrían morir).
En la tecnología, existen umbrales a partir de los cuales las cosas pueden prenderse, apagarse o hacer algo. Por ejemplo, los diodos de silicio obedecen a la desigualdad si V<0.7 no conduce, si V>0.7 conduce. Si fuera de germanio seria con 0.3V.
En la naturaleza todo obedece las leyes de mínimo esfuerzo y energía, como las leyes Clasius, los procesos espontáneos, la entropía, etc; cuyas condiciones se expresan con desigualdades